文章目录
一. deque简单介绍
1.1 deque的功能介绍
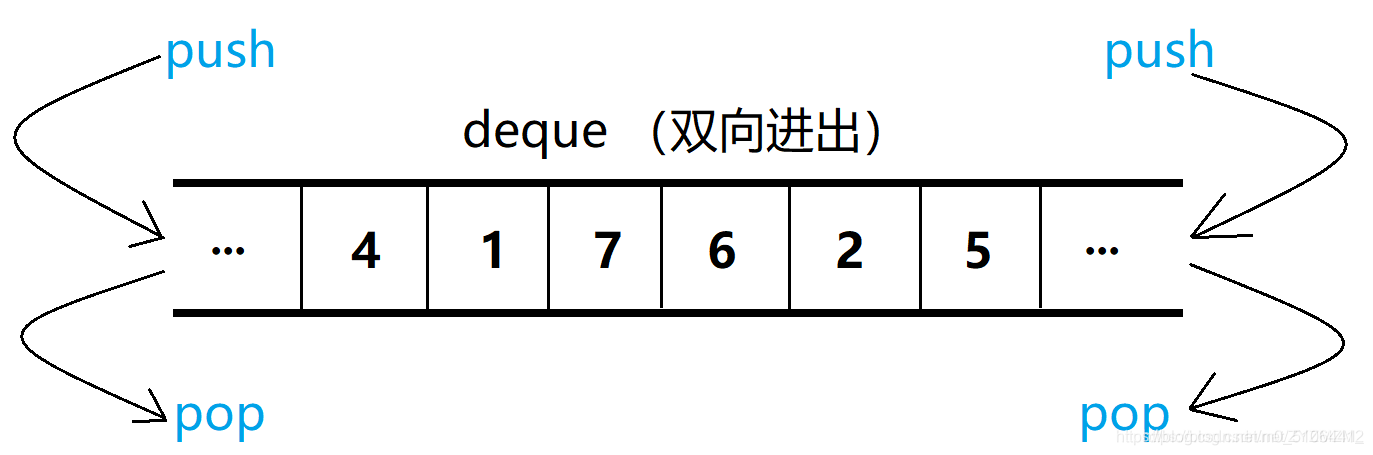
deque(双端队列):是一种双开口的连续空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要挪动元素;与list比较,空间利用率比较高。
1.2 deque的本体框架
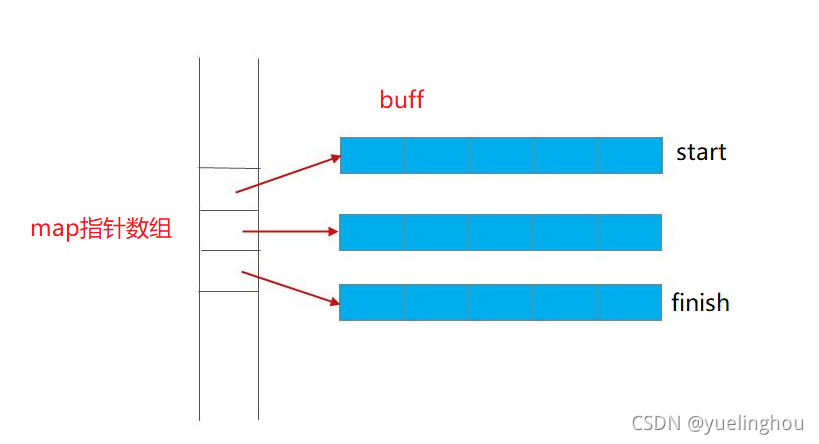
虽说是连续性存储空间,但这种连续性只是表面上的,实际上它在堆上分配了一块一块的动态储存区,叫做缓冲区(buff),每一块缓冲区本身是连续的,deque自身的机制把这一块一块的缓冲区虚拟地连在一起,即把它们的首元素地址存在一个指针数组map里,注意这里的map不是STL里的map容器,而是deque的中控器,是个指针数组。
template<class T>
class deque
{
protected:
iterator start; // 指向指针数组第一个元素的迭代器
iterator finish;// 指向指针数组最后一个元素的迭代器
T** map; // 中控的指针数组
size_t map_size;// 指针数组大小
};
为了满足头尾的插入删除,一开始的buff会放到中间位置,这样如果有需要的话,往前往后都可以存buff。当map指向的这块空间不够存放内存指针的时候,就会另觅一块更大的连续性空间,然后把指针一个一个复制过去,并销毁旧的空间。利用这种数据结构,deque就能方便地模拟自身的存储区是连续性空间的假象,并且可以实现双向插入删除的功能。
1.3 deque的迭代器框架
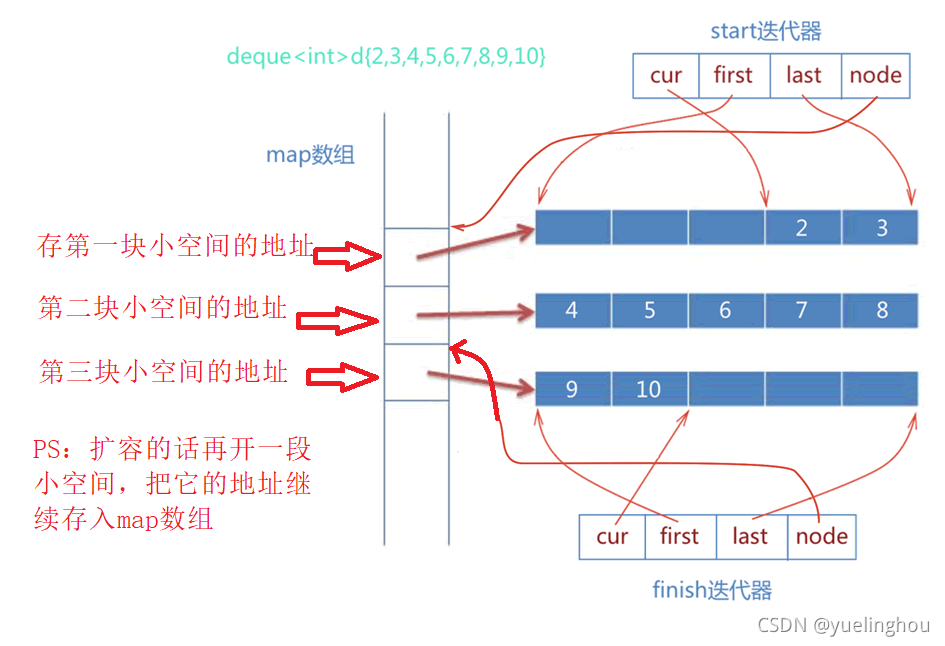
迭代器就是模拟指针的操作,比如解引用得到具体的数据,箭头访问内部成员变量,自增、自减等等操作。那么deque的迭代器应该具备怎么结构?我们可以考虑以下几点。首先,需要知道该元素位于哪个buff的哪个位置;其次,一旦迭代器前进和后退有可能会跳跃至上一个或下一个缓冲区,为了判断跳跃的条件就需要知道,当前元素所在buff的首尾指针。最后,如果前进或后退必须跳跃至下一个或上一个缓冲区。为了能够正确跳跃,deque必须随时掌握管控中心(map),通过map可以知道跳跃的缓冲区。 所以在迭代器中需要定义如下参数:
template<class T, class Ref, class Ptr, size_t N>
struct _deque_iterator
{
T* cur; //指向buff里面当前数据的位置
T* first;//buff第一个位置指针
T* last; //buff最后一个位置指针
T** node;//map中控中当前buff的地址
}
迭代器和中控器之间的关系如下图所示
1.2 deque的优缺点
优点
- 与vector相比:头部和中间的插入删除不需要大量挪动数据,时间复杂的为O(1);扩容时也不需要大量挪动数据。
- 与list相比:空间利用率较高,内存碎片少,不是需要一个才开辟一个。
缺点
不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下。
总结
因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构。
二. 容器适配器
2.1 什么是适配器
适配器是一种设计模式,该种模式是将一个类进行封装,利用原来类的接口转换成客户希望的另外一个接口。
2.2 STL标准库中的stack和queue底层结构
虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配器,这是因为stack和队列只是对其他容器的接口进行了包装,其中STL中stack和queue默认容器使用deque。


2.3 stack和queue的模拟实现
2.3.1 stack容器剖析
两者的实现原理一样,下面我们主要分析stack的实现
stack要做到存储不同类型数据,那就应该是个类模板,模板参数是要存储的数据的类型和底层容器的种类。

注意:容器也是可以作为模板参数的,因为模板作用就是处理不同类型但逻辑相同的问题,我们对传入的不同类型统一管理,像vector,list等容器算自定义类型,我们也可以作为模板参数传入。
stack的框架
成员变量只有一个,就是底层的容器的一个实例化对象
// 这里我们的底层容器默认缺省是deque
template<class T, class Container = deque<T>>
class stack
{
public:
// 构造函数
stack()
// 调用容器的无参的默认构造函数
:_con()
{}
private:
// 底层结构,即容器对象
Container _con;
};
入栈
只能栈顶入数据,就是deque的尾插,对应调用底层容器deque的push_back()
PS:直接调用就行,不用考虑空间不够增容的问题,这些归底层容器deque管
// 入栈
void push(const T& data)
{
_con.push_back(data);
}
出栈
从栈顶出,就是deque的尾删,封装deque的back_pop()
// 出栈
void pop()
{
_con.pop_back();
}
获取栈顶元素
就是获取deque的最后一个元素,这里要注意不同stack对象调用对应的返回值不同,所以有下面两种写法:const的栈对象返回const的值,非const的栈对象返回非const的值。
// 普通对象获取栈顶元素
T& top()
{
return _con.back();
}
// const对象获取栈顶元素
const T& top()const
{
return _con.back();
}
stack的完整模拟实现
template<class T,class Container=deque<T>>
class stack
{
public:
// 构造函数
stack()
:_con()
{}
// 入栈
void push(const T& data)
{
_con.push_back(data);
}
// 出栈
void pop()
{
_con.pop_back();
}
// 判空
bool empty()
{
return _con.empty();
}
// 长度
size_t size()
{
return _con.size();
}
// 普通对象获取栈顶元素
T& top()
{
return _con.back();
}
// const对象获取栈顶元素
const T& top()const
{
return _con.back();
}
private:
// 底层容器
Container _con;
};
2.3.2 queue的完整模拟实现
与stack大同小异,由于两者的特性不同(stack是后进先出,queue是先进先出),对应容器调用的接口也就不一样。
template<class T,class Container=deque<T>>
class queue
{
public:
// 构造函数
queue()
:_con()
{}
// 队列尾部插入元素
void push(const T& data)
{
_con.push_back(data);
}
// 队列头部出元素
void pop()
{
_con.pop_front();
}
// 返回队列当前元素个数
size_t size()
{
return _con.size();
}
// 判断队列是否为空
bool empty()
{
return _con.empty();
}
// 普通对象直接返回对头元素的引用(可修改)
T& front()
{
return _con.front();
}
// const对象返回对偷的元素不能修改
const T& front()const
{
return _con.front();
}
// 普通对象直接返回对尾元素的引用(可修改)
T& back()
{
return _con.back();
}
// const对象返回对尾的元素不能修改
const T& back()const
{
return _con.back();
}
private:
Container _con;
};
三. priority_queue
3.1 priority_queue介绍
- 优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆。所有需要用到堆的场景,都可以考虑使用priority_queue(注意默认情况下priority_queue是大堆)
- 它的接口和栈的接口类似
push():数据进堆
pop():删除堆顶数据
top():拿到堆顶数据
empty():堆是否为空?为空的话返回true,不空返回false
size():当前堆元素的数量
3.2 priority_queue的模拟实现
PS:容器vector的数据位置要用到堆结构处理,堆的知识和相关堆算法,这些堆的内容可以参考下面文章:二叉树和堆
仿函数:
定义一个类专门重载operator(),使该类实例化出来的对象可以像调用函数一样的调用,从而实现特定功能,你如比较两个数据的大小。

priority的基本框架
-
模板参数,除了数据类型和容器,还加了仿函数类Compare,为了使用户可以自主选择大堆和小堆才引入的,当然默认情况是大堆,根STL里一致,大堆传less的仿函数,小堆传greater

-
仿函数我们在priority_queue外单独定义
// 仿函数less
template<class T>
struct less
{
bool operator()(const T& x1, const T& x2)
{
return x1 < x2;
}
};
// 仿函数greater
template<class T>
struct greater
{
bool operator()(const T& x1, const T& x2)
{
return x1 > x2;
}
};
// priority_queue
template<class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
// 无参的默认构造函数
priority_queue()
:_con()
{}
private:
Container _con;
};
堆的向上和向下调整算法
我们尾部插入元素要利用向上调整算法调堆,删除堆顶元素要用向下调整算法调堆。只是在插入和删除操作时调用,一般外部不用直接调用(因为没意义),所以我们把这两个算法设置成私有。
但不能把他们设置为内联,因为他们内部有循环操作,且代码较长。
private:
// 向下调整算法
void AdjustDown(int parent)
{
int n = _con.size();
int child = parent * 2 + 1;
while(child < n)
{
if (child + 1 < n&&Compare()(_con[child], _con[child + 1]))
{
++child;
}
if (Compare()(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
return;
}
}
}
// 向上调整算法
void AdjustUp(int child)
{
int n = _con.size();
while (child > 0)
{
int parent = (child - 1) / 2;
if (Compare()(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
child = parent;
}
else
{
return;
}
}
}
Container _con;
用迭代器区间构造一个priority_queue对象
像下图一样构造一个优先级队列的对象

template<class Iterator>
priority_queue(Iterator first, Iterator last)
// 先把数据存入容器对象
: _con(first, last)
{
// 向下调整法建堆
int n = _con.size();
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(i);
}
}
入队列
就是vector的尾插,再把插入的元素向上调整,保持堆的结构
// 入队列
void push(const T& data)
{
_con.push_back(data);
AdjustUp(_con.size()-1);
}
出队列
删除堆顶元素。交换一下堆顶和堆底元素,不用重新建堆,vector尾删,最后在给堆顶元素进行向下调整算法。
// 出队列
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
AdjustDown(0);
}
获取堆顶元素
堆顶元素不允许修改,因为:堆顶元素修改可以会破坏堆的特性。
// 获取栈顶(堆顶)元素
const T& top()const
{
return _con.front();
}

完整代码
#include<iostream>
#include<vector>
using namespace std;
namespace MyPriorityQueue
{
// 仿函数less
template<class T>
struct less
{
bool operator()(const T& x1, const T& x2)
{
return x1 < x2;
}
};
// 仿函数greater
template<class T>
struct greater
{
bool operator()(const T& x1, const T& x2)
{
return x1 > x2;
}
};
// priority_queue
template<class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
// 无参的默认构造函数
priority_queue()
:_con()
{}
// 传迭代对应容器类型对象的迭代器来构造
template<class Iterator>
priority_queue(Iterator first, Iterator last)
: _con(first, last)
{
// 向下调整法建堆
int n = _con.size();
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(i);
}
}
// 入队列
void push(const T& data)
{
_con.push_back(data);
AdjustUp(_con.size()-1);
}
// 出队列
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
AdjustDown(0);
}
// 长度
int size()const
{
return _con.size();
}
// 判空
bool empty()const
{
return _con.empty();
}
// 获取栈顶(堆顶)元素
const T& top()const
{
return _con.front();
}
private:
// 向下调整算法
void AdjustDown(int parent)
{
int n = _con.size();
int child = parent * 2 + 1;
while(child < n)
{
if (child + 1 < n&&Compare()(_con[child], _con[child + 1]))
{
++child;
}
if (Compare()(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
return;
}
}
}
// 向上调整算法
void AdjustUp(int child)
{
int n = _con.size();
while (child > 0)
{
int parent = (child - 1) / 2;
if (Compare()(_con[parent], _con[child]))
{
swap(_con[parent], _con[child]);
child = parent;
}
else
{
return;
}
}
}
private:
Container _con;
};
void test()
{
vector<int> v = { 2,1,3,3,2,0,6 };
priority_queue<int> p(v.begin(), v.end());
}
}