文章目录
1. 分布式系统的时间
1.1. 计算机时钟
计算机时钟有两种:
- 硬件时钟
硬件时钟是指计算机内的时钟硬件计算出来的时间 H ( t ) H(t) H(t)。用于机器硬件同步,特别是流水线作业,一般用户不用管它如何工作,是硬件层的东西。 - 软件时钟
软件时钟是指操作系统在启动时读取的硬件时钟 C ( t ) = α H ( t ) + β C(t)=\alpha H(t)+\beta C(t)=αH(t)+β,读取后独立运行,与硬件时钟无关。用于给用户展示、本质上是操作系统层的东西。
分布式系统中的每个计算机有它自己的时钟,本地进程可用它获得当前时间。但由于计算机时钟与完美时钟有漂移,它们的漂移率各不相同,导致不同计算机上的时钟可能给出不同的时间,这使得在不同计算机上,进程能用本地时间给事件打上时间戳在分布式系统内可能造成时间混乱。
时钟漂移,是指时钟的绝对偏差;
漂移率,是指漂移的程度,石英钟是 1 0 ? 6 s / s 10^{-6}s/s 10?6s/s,即每1000000秒或11.6天有1秒的差别。
另一方面,由于计算机硬件本身有质量差别,即使分布式系统中所有计算机的时钟被设成相同时间,它们的时钟如果不做校正最终也会相差很大。
1.2. 时间同步
要在分布式系统内进行时间同步,首先就要判断单个机器的时间是否正确,只有时间是正确的,才能进行有效同步。
时间正确的三个性质:
- 时钟正确性
如果一个硬件时钟 H H H的漂移率在一个已知的范围 ρ > 0 \rho >0 ρ>0 内,那么这个硬件时钟 H H H是正确的; - 硬件时钟的误差有界性
满足 ( 1 ? ρ ) ( t ′ ? t ) ≤ H ( t ′ ) ? H ( t ) ≤ ( 1 + ρ ) ( t ′ ? t ) (1-\rho)(t'-t)\leq H(t')-H(t) \leq (1+\rho)(t'-t) (1?ρ)(t′?t)≤H(t′)?H(t)≤(1+ρ)(t′?t),其中 t ′ 、 t , ( t ′ > t ) t'、t,(t'>t) t′、t,(t′>t)是实际时间, H ( t ′ ) 、 H ( t ) H(t')、H(t) H(t′)、H(t)是相应的硬件时钟值。 - 软件时钟的单调性
满足 C ( t ′ ) ≥ C ( t ) C(t')\geq C(t) C(t′)≥C(t),其中 t ′ 、 t , ( t ′ > t ) t'、t,(t'>t) t′、t,(t′>t)是实际时间, C ( t ′ ) 、 C ( t ) C(t')、C(t) C(t′)、C(t)是相应的软件时钟值。
在有了正确时间之后,就可以进行时间同步了。时间同步分为两种:
- 外部同步
用权威的外部时间源同步进程的时钟 - 内部同步
内部同步的时钟未必是外部同步的,因为即使它们相互一致,它们整体上也可能都与时间的外部源有偏差。如果系统在范围 D D D内是外部同步的,那么同一系统在范围 2 D 2D 2D内是内部同步的,原因很简单,假设外部时间源的时间是 t t t,那么外部时间的最大差值范围就是 D = ( t , t + Δ t ) D=(t, t+\Delta t) D=(t,t+Δt)或 ( t ? Δ t , t ) (t-\Delta t,t) (t?Δt,t),内部时间的最大差值范围就是 2 D = ( t ? Δ t , t + Δ t ) 2D=(t-\Delta t,t+\Delta t) 2D=(t?Δt,t+Δt)。
首先,在计算机系统中,当时间快了时,要逐步回拨,渐渐靠近正确时间,而不能一步到位,因为会违反时间单调性;当时间慢了时,可以直接将时间拨到正确时间。
1.3. 分布式系统的时间分类
- 同步系统
已知时钟漂移率的范围、已知最大的消息传输延迟、已知进程每一步的执行时间就可以构建一个同步分布式系统; - 异步系统
在时钟漂移、消息传输延迟和进程执行时间上没有限制的系统只能是一个异步系统。
2. 同步系统的时间同步
2.1. Cristian外部同步方法
Cristian方法使用一个有标准时间的服务器 S S S,通过计算消息的往返时间来完成同步,该方法要求往返时间不能过长,否则同步的频率过大会导致同步失败。
同步流程:
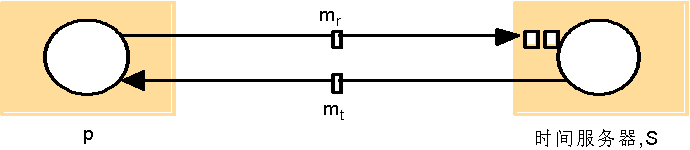
- 计算机进程 p p p 在发给 S S S 的消息 m r m_r mr? 中请求获得准确的时间;
- S S S 在返回的消息 m t m_t mt?上放置准确的时间值 t t t;
- p p p 从返回的消息 m t m_t mt?中接收准确的时间值 t t t,同时记算了发出消息到返回消息的往返时间差 T r o u n d T_{round} Tround?;
- p p p 设置它的时钟时间为 t + T r o u n d 2 t+\frac{T_{round}}{2} t+2Tround??。
同步精度(时钟偏移的边界)分析:
假设
p
p
p与
S
S
S之间的最小传输时间为
min
?
\min
min,注意
min
?
≠
T
r
o
u
n
d
2
\min \neq \frac{T_{round}}{2}
min?=2Tround??,因为
T
r
o
u
n
d
2
\frac{T_{round}}{2}
2Tround??是实际时间,
min
?
\min
min是理论最小值。
由于放置时间 t t t后,影响 p p p与 S S S同步的时间只有 m t m_t mt?。那么很显然,当 T r o u n d T_{round} Tround?确定时:
-
m
t
m_t
mt? 取最小值
min
?
\min
min 时
p p p接收到 m t m_t mt?时, S S S的实际时间是 t + min ? t+\min t+min -
m
t
m_t
mt? 取最大值
T
r
o
u
n
d
?
min
?
T_{round}-\min
Tround??min 时
p p p接收到 m t m_t mt?时, S S S的实际时间是 t + T r o u n d ? min ? t+T_{round}-\min t+Tround??min
所以, S S S的时钟时间在范围 [ t + min ? , t + T r o u n d ? min ? ] [t+\min, t+T_{round}-\min] [t+min,t+Tround??min]内,则 p p p 的的时钟时间范围在: [ t + min ? + T r o u n d 2 , t + T r o u n d ? min ? + T r o u n d 2 ] = [ t + T r o u n d 2 + min ? , t + 3 T r o u n d 2 ? min ? ] [t+\min+\frac{T_{round}}{2}, t+T_{round}-\min+\frac{T_{round}}{2}]=[t+\frac{T_{round}}{2}+\min, t+\frac{3T_{round}}{2}-\min] [t+min+2Tround??,t+Tround??min+2Tround??]=[t+2Tround??+min,t+23Tround???min]内。
同步时间宽度为:
(
t
+
3
T
r
o
u
n
d
2
?
min
?
)
?
(
t
+
T
r
o
u
n
d
2
+
min
?
)
=
T
r
o
u
n
d
?
2
min
?
(t+\frac{3T_{round}}{2}-\min)-(t+\frac{T_{round}}{2}+\min)=T_{round}-2\min
(t+23Tround???min)?(t+2Tround??+min)=Tround??2min;
同步时间精确度为:
±
1
2
(
T
r
o
u
n
d
?
2
min
?
)
=
±
(
T
r
o
u
n
d
2
+
min
?
)
\pm\frac{1}{2}(T_{round}-2\min)=\pm (\frac{T_{round}}{2}+\min)
±21?(Tround??2min)=±(2Tround??+min)
2.2. Berkeley内部同步方法
Berkeley算法是一种用于分布式集群内部计算机之间的同步方法。
同步流程:
- 在计算机集群中,选择一台作为 Master 计算机;
- Master 周期性地轮询其他要进行时钟同步的Slave计算机;
- Slave将它们的时钟值返回给Master;
- Master 根据数据往返时间差计算它们的本地时钟时间,并计算这些时间差的平均值;
- Master 给每个Slave 发送时钟所需的调整量。
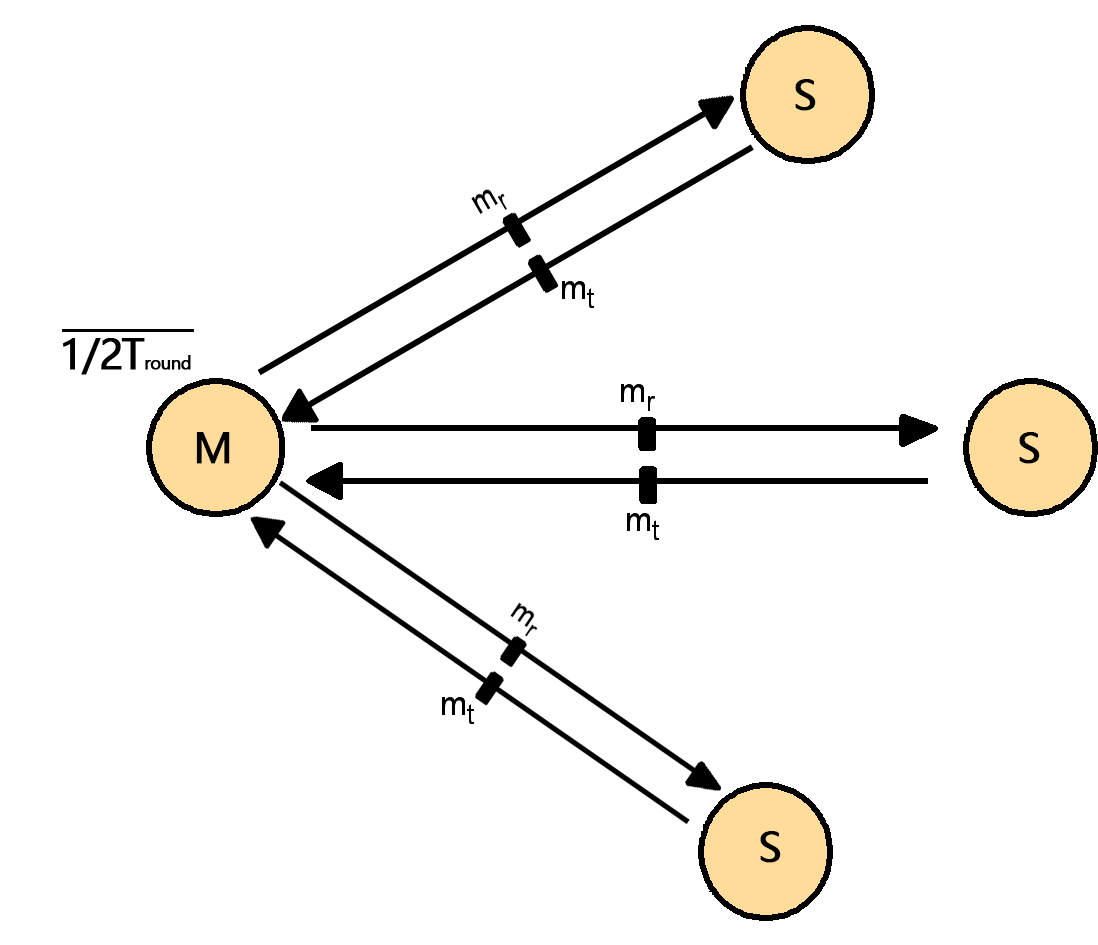
Berkeley算法的容错能力强,(1)算法容许有计算机拥有错误的时钟,因为Master采用了平均值来实现容错机制,同时还可以设置范围值消除异常的往返时间;(2)算法容许Master崩溃,崩溃后新的Master通过选举算法产生。
与Cristian相似,Berkeley同步的精确度取决于Master-Slave之间的最大往返时间。
3. 网络时间协议 NTP
3.1. NTP的设计目标
NTP(Network Time Protocol)定义了时间服务的体系结构和在Internet上发送时间信息的协议。
NTP的设计目标包括:
- 提供一个用统计方法来过滤时序数据的服务,使得Internet上的用户能精确地同标准时间同步;
- 使得客户能经常有效地重新同步以抵消在大多数计算机中存在的漂移率,该服务具有对数据庞大的客户和服务器的可伸缩性;
- 能够在不可靠的通信链接上提供一个可靠的服务:通过提供冗余的服务器以及服务器之间冗余的路径。如果其中一个不可达,服务器能重新进行配置以便继续提供服务;
- 通过使用使用认证技术,防止恶意或偶然的时间服务干扰。
3.2. NTP的体系结构
NTP的体系结构如下:
- NTP的同步子网是用Bellman-Ford路由算法的变种方法来组织的,构建以主服务器为根的最小权重的支撑树;
- 主(根)服务器直接连到外部时间源,下一层的服务器与主服务器同步,再下一层的服务器与上一层的服务器同步等等。
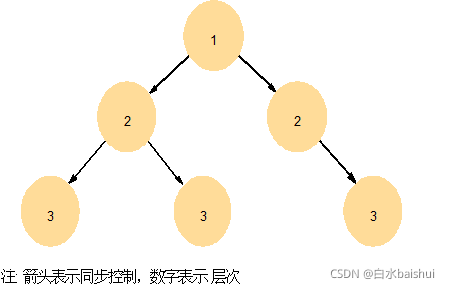
这样的结构有助于故障处理,同步子网可以进行重新配置,以应对服务器不可达或出现故障。例如如果主服务器的外部时间源出现故障,那么它能变成层次2的二级服务器,新的主服务器会从原先的从服务器中选定。
3.3. NTP的同步方式
NTP服务器按三种模式中的一种相互同步:组播、过程调用、对称模式。这三种模式都是使用UDP协议进行数据传输的。
- 组播模式
组播模式适用于高速LAN环境。该模式在低延迟下,一个或多个标准时间服务器会周期性地将时间组播到其他服务器,并设置它们的时钟。 - 过程调用模式
过程调用模式适用于精确性要求比组播更高的地方,或不能用硬件支持组播的地方。该模式类似Cristian算法的操作,一个服务器接收来自其他计算机请求,并用时间戳(本地的当前的时钟读数)应答。 - 对称模式
对称模式适用于在LAN中提供时间信息的服务器和同步子网的较高层,即要获得最高精确性的地方。该模式用一对服务器相互交换有时序信息的消息。
在NTP中,每个消息携带3个时间戳:发送前一个NTP消息的本地时间、接收前一个NTP消息的本地时间、发送当前消息的本地时间。有了这三个时间,就能计算出所有同步需要的时间。
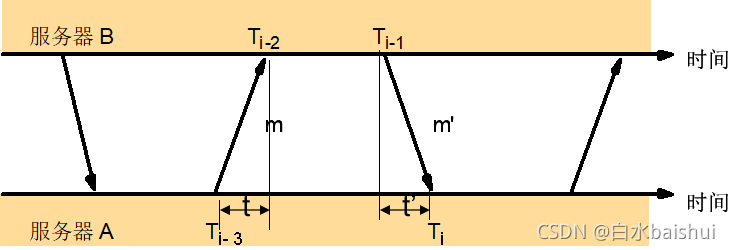
如上图, m m m 和 m ′ m' m′ 实际的传输时间分别是 t t t 和 t ′ t' t′, d i d_i di? 是两个消息往返的传输时间,设 B B B 上时钟相对于 A A A 的真正偏移量是 o o o, o i o_i oi?是偏移(clock offset)的估计。
T i ? 2 = T i ? 3 + t + o , T i = T i ? 1 + t ′ + o T_{i-2}=T_{i-3}+t+o,\qquad T_{i}=T_{i-1}+t'+o Ti?2?=Ti?3?+t+o,Ti?=Ti?1?+t′+o d i = t + t ′ = T i ? 2 ? T i ? 3 + T i ? T i ? 1 d_i=t+t'=T_{i-2}-T_{i-3}+T_{i}-T_{i-1} di?=t+t′=Ti?2??Ti?3?+Ti??Ti?1? o = o i + ( t ′ ? t ) / 2 , w h e r e o i = ( T i ? 2 ? T i ? 3 + T i ? T i ? 1 ) / 2 o=o_i+(t'-t)/2,\quad where\quad o_i=(T_{i-2}-T_{i-3}+T_{i}-T_{i-1})/2 o=oi?+(t′?t)/2,whereoi?=(Ti?2??Ti?3?+Ti??Ti?1?)/2由以上计算式,可得: o i ? d i / 2 ≤ o ≤ o i + d i / 2 o_i-d_i/2\leq o\leq o_i+d_i/2 oi??di?/2≤o≤oi?+di?/2可知,当 d i d_i di? 越小,偏移量 o o o就越精准。因此要选具有最小 d i d_i di?值的 o i o_i oi?值用于估计 o o o。
同步流程:
- 以时间服务器 P e e r Peer Peer 在NTP树结构中的层次和离主(根)服务器的同步距离对所有 P e e r Peer Peer 进行排序,假设排序为 P 1 ? P 2 ? P 3 P1-P2-P3 P1?P2?P3,即 P 1 P1 P1 最优;
- 一台待同步服务器 Q Q Q 向多台时间服务器 p e e r peer peer 传输数据,过程中会产生大量的 < d i , j , o i , j > <d_{i,j},o_{i,j}> <di,j?,oi,j?>对;
- 每组
<
d
i
,
o
i
>
<d_{i},o_{i}>
<di?,oi?>对按照
d
j
d_{j}
dj?升序排列,然后每个
P
e
e
r
Peer
Peer选择最小
d
i
,
j
d_{i,j}
di,j?对应的
o
i
,
j
o_{i,j}
oi,j?作为本服务器的第一候选偏移量(如下图蓝色
o
i
,
j
o_{i,j}
oi,j?)。
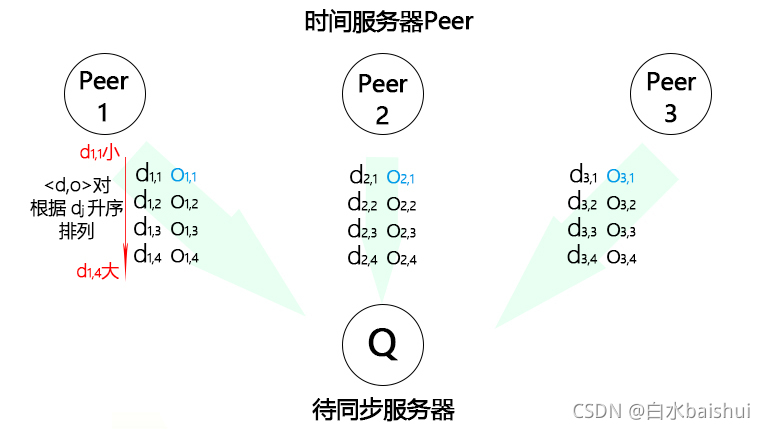
- 然后计算每个 P e e r Peer Peer和 Q Q Q之间时间偏差的离散程度: ? i = ∑ j = 1 n ( o i , j ? o i , 1 ) v j = ( o 1 , 1 ? o 1 , 1 ) v 1 + ( o 1 , 2 ? o 1 , 1 ) v 2 + . . . \epsilon^i=\sum_{j=1}^{n}(o_{i,j}-o_{i,1})v^j=(o_{1,1}-o_{1,1})v^1+(o_{1,2}-o_{1,1})v^2+... ?i=j=1∑n?(oi,j??oi,1?)vj=(o1,1??o1,1?)v1+(o1,2??o1,1?)v2+...其中, n n n是每组 < d i , j , o i , j > <d_{i,j},o_{i,j}> <di,j?,oi,j?>的数量; v j v^j vj是对应的权重,参考值是0.5。
- 然后再计算所有候选偏移量时间偏差的离散程度: ? i = ∑ i = 1 m ( o 1 , 1 ? o i , 1 ) v i = ( o 1 , 1 ? o 2 , 1 ) w 1 + ( o 1 , 1 ? o 3 , 1 ) w 2 + . . . \epsilon_i=\sum_{i=1}^{m}(o_{1,1}-o_{i,1})v^i=(o_{1,1}-o_{2,1})w^1+(o_{1,1}-o_{3,1})w^2+... ?i?=i=1∑m?(o1,1??oi,1?)vi=(o1,1??o2,1?)w1+(o1,1??o3,1?)w2+...其中, m m m是候选偏移量的数量; w i w_i wi?是对应权重,参考值是0.75。
- 分别计算出
Q
Q
Q 对应
P
e
e
r
Peer
Peer 的
?
i
\epsilon^i
?i 和
?
i
\epsilon_i
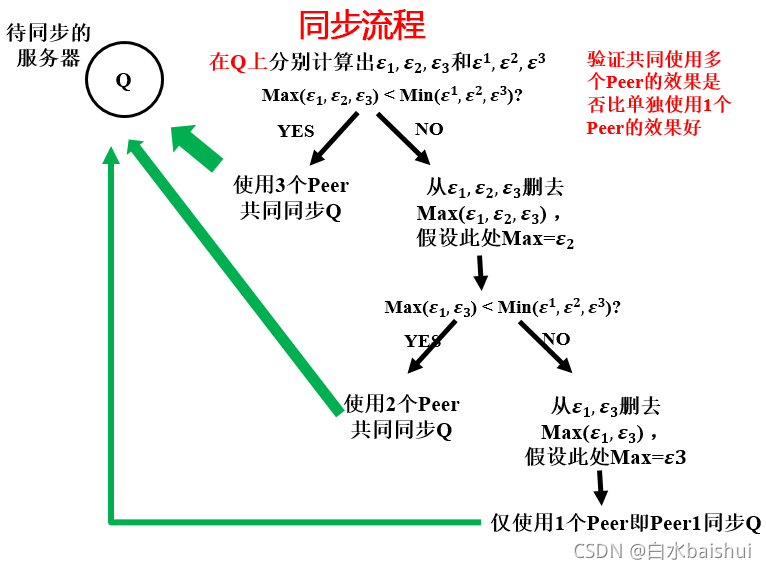
?i?后,就开始验证应该用多少个Peer同步Q上的时间。做法就是,不断比较
max
?
(
?
1
,
?
2
,
.
.
.
,
?
m
)
<
min
?
(
?
1
,
?
2
,
.
.
.
,
?
n
)
\max(\epsilon_1,\epsilon_2,...,\epsilon_m)<\min(\epsilon^1,\epsilon^2,...,\epsilon^n)
max(?1?,?2?,...,?m?)<min(?1,?2,...,?n)若满足,则使用
?
1
,
?
2
,
.
.
.
,
?
m
\epsilon_1,\epsilon_2,...,\epsilon_m
?1?,?2?,...,?m?的均值来同步Q的时间;若不满足,则从
?
1
,
?
2
,
.
.
.
,
?
m
\epsilon_1,\epsilon_2,...,\epsilon_m
?1?,?2?,...,?m?取出最大值,重新比较,如此往复。直到最后只剩一个
?
i
\epsilon_i
?i?,则使用该值更新Q的时间。
4. 时钟算法
4.1. 事件排序
将事件发生的先后关系(happened-before)进行排序,那么该事件排序有三种性质:
- 若在进程 i i i中先发生了事件 e e e,后发生了事件 e ′ e' e′,则有 e → i e ′ e\to_i e' e→i?e′(或表达为 e → e ′ e\to e' e→e′)。其中 → i \to_i →i?特指同一个进程中两个事件的顺序发生关系;
- 对于任意消息 m m m,一定有 s e n d ( m ) → r e c e i v e ( m ) send(m)\to receive(m) send(m)→receive(m),即发送消息在前,接收消息在后;
- 若事件 e e e、 e ′ e' e′、 e ′ ′ e'' e′′按时间顺序先后发生,即 e → e ′ e\to e' e→e′、 e ′ → e ′ ′ e'\to e'' e′→e′′,则有 e → e ′ ′ e\to e'' e→e′′。
很显然,事件之间的
→
\to
→关系捕获了以消息传递方式表示的数据流,如下图:
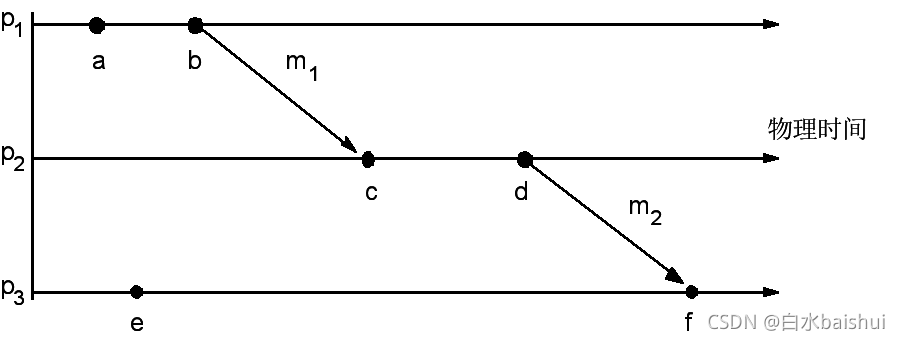
需要注意的是, → \to →描述的是时间顺序关系,而不是因果关系,用 → \to →来描述的两个事件即使没有真正的因果调用关系,也可以有时间顺序上的关系。不能由 → \to →排序的事件是并发的事件,如上图中的 a a a和 e e e之间没有 → \to →关系。
4.2. Lamport逻辑时钟
Lamport逻辑时钟将逻辑时钟定义为一个单调增长的软件计数器。
在实现上,设定每个进程 p i p_i pi?维护一个独立的逻辑时钟 L i L_i Li?,进程用它给事件加时间戳:
- 用 L i ( e ) L_i(e) Li?(e)表示进程 p i p_i pi?发生的事件 e e e的时间戳;
- 用 L ( e ) L(e) L(e)表示发生任一进程中的事件 e e e的时间戳。
由此,逻辑时钟计算规则定义为:
- 在进程 p i p_i pi?进行 s e n d ( m ) send(m) send(m)事件之前, L i L_i Li?加一: L i : = L i + 1 L_i:=L_i+1 Li?:=Li?+1;
- 当进程 p i p_i pi?进行 s e n d ( m ) send(m) send(m)事件时,设置 s e n d ( m ) send(m) send(m)事件的时间戳为 t = L i t=L_i t=Li?,组成 ( m , t ) (m,t) (m,t);
- 另一进程 p j p_j pj?进行 r e c e i v e ( m ) receive(m) receive(m)事件时,计算 L j : = max ? ( L j , t ) L_j:=\max(L_j,t) Lj?:=max(Lj?,t),并设置 r e c e i v e ( m ) receive(m) receive(m)事件的时间戳为 L j : = L j + 1 L_j:=L_j+1 Lj?:=Lj?+1
逻辑时钟值不能区分是由于局部事件引起的时钟前进还是由于进程间的消息交换引起的时钟前进,因此也就有:
- 若 e → e ′ e\to e' e→e′,则能推出 L ( e ) < L ( e ′ ) L(e)<L(e') L(e)<L(e′);
- 若 L ( e ) < L ( e ′ ) L(e)<L(e') L(e)<L(e′),不能推出 e → e ′ e\to e' e→e′。
4.3. 向量时钟
向量时钟定义为:若系统中有 N N N个进程,每个进程 p i p_i pi?和构造一个向量 V i [ 1 , . . . , i , . . , n ] V_i[1,...,i,..,n] Vi?[1,...,i,..,n],并相关联,该向量用于给本地事件加时间戳,1…n分别对应着每一个进程号。举例说明:
- V i [ i ] V_i[i] Vi?[i]是当前进程 i i i中,进程 i i i已经加了时间戳的事件的个数;
- V i [ j ] V_i[j] Vi?[j]是当前进程 i i i中,进程 j j j已经加了时间戳的事件的个数;
- V i = ( 5 , 9 , 0 ) V_i=(5,9,0) Vi?=(5,9,0)是当前进程 i i i中,进程 1 1 1有5个事件被加上了时间戳,进程2有9个事件被加上了时间戳,进程3有0个事件被加上了时间戳;
由此,向量时钟计算规则定义为:
- 对进程 p i p_i pi?初始化一个零向量 V i [ 1 , . . . , i , . . , n ] V_i[1,...,i,..,n] Vi?[1,...,i,..,n];
- 进程 p i p_i pi?在进行 s e n d ( m ) send(m) send(m)事件之前,设置 V i [ i ] = V i [ i ] + 1 V_i[i]=V_i[i]+1 Vi?[i]=Vi?[i]+1;
- 当进程 p i p_i pi?进行 s e n d ( m ) send(m) send(m)事件时,设置 s e n d ( m ) send(m) send(m)事件的时间戳为 t = V i t=V_i t=Vi?,组成 ( m , t ) (m,t) (m,t);
- 另一进程 p j p_j pj?进行 r e c e i v e ( m ) receive(m) receive(m)事件时,对 p j p_j pj?的向量 V j V_j Vj?进行更新: V j [ k ] = max ? ( V j [ k ] , t [ k ] ) k = 1 , . . . , n V_j[\mathtt{k}]=\max(V_j[\mathtt{k}],t[\mathtt{k}])\quad \mathtt{k}=1,...,n Vj?[k]=max(Vj?[k],t[k])k=1,...,n。
例如下图: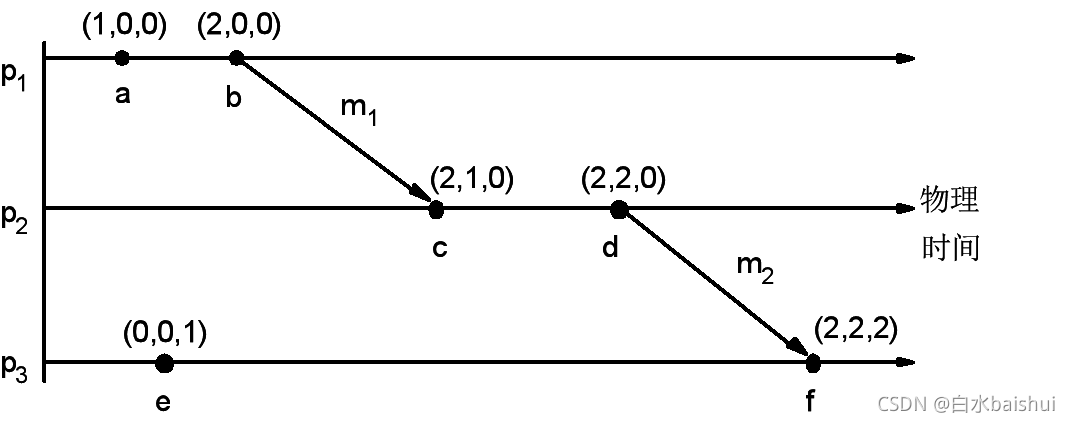
向量时钟可以在发生在先关系和向量时钟之间建立等价关系:
- 若 e → e ′ e\to e' e→e′,则能推出 L ( e ) < L ( e ′ ) L(e)<L(e') L(e)<L(e′);
- 若 L ( e ) < L ( e ′ ) L(e)<L(e') L(e)<L(e′),也能推出 e → e ′ e\to e' e→e′。