1 简介
智能交通系统的研究主要是为了建立现代化交通运输系统和交通信息管理系统,而其中的核心领域之一就是动态网络分配模型和算法。基于经典的 NaSch 模型,本文对模拟交通路网的元胞自动机模型进行了深入研究,提出了两类新模型,即车道元胞自动机模型和交叉口元胞自动机模型。本文详细阐明了路径搜索原则,当问题从一维变为二维时,还加入了交叉口模型以及转向模型,得到了一套自适应的交通网模拟系统,从而根据其中的数据以及当前所研究的各种动态网络分配模型定义了该系统的双目标函数,并采用 NSGA—II 算法对该双目标规划模型进行了求解。此外,本文还对一个二维路网进行了数值模拟,并对模拟结果进行了详细分析。研究结果表明本文提出的模型可以较好的用于动态网络分配。数值实验结果表明,在对交通网络基于完善规则的模拟的情况下,应用恰当的算法可以对交通网进行一定程度的优化。




2 部分代码
function s = goforward(s,m,i,T,p,vmax)%此处的p是转弯概率if mod(i,sum(T))<=T(1)-1flag=1;elseflag=2;end[a,b]=size(s{1});%右行right=s{1}.*(m==1);[right_1,right_2]=find(right);[right_2,i_r]=sort(right_2,'descend');right_1=right_1(i_r);for i=1:length(right_1)v=0;leave=0;incross=0;for v_i=1:vmaxif right_2(i)+v_i>bs{1}(right_1(i),right_2(i))=0;s{2}(right_1(i),right_2(i))=0;%s{3}(right_1(i),right_2(i))=0;leave=1;break;endlight=~((flag==2)&(m(right_1(i),right_2(i)+v_i)==6));if s{1}(right_1(i),right_2(i)+v_i)==0 && lightv=v_i;if m(right_1(i),right_2(i)+v_i)==5 ...||m(right_1(i),right_2(i)+v_i)==6incross=1;break;endelsebreak;endendif leave==0 %没有离开才有这些v=min(v,s{2}(right_1(i),right_2(i))+1);s{1}(right_1(i),right_2(i))=0;s{1}(right_1(i),right_2(i)+v)=1;if incross~=1s{2}(right_1(i),right_2(i)+v)=v;elses{2}(right_1(i),right_2(i)+v)=max(s{2}(right_1(i),right_2(i)),v);ends{2}(right_1(i),right_2(i))=0;endend%左行left=s{1}.*(m==2);[left_1,left_2]=find(left);[left_2,i_r]=sort(left_2);left_1=left_1(i_r);for i=1:length(left_1)v=0;leave=0;incross=0;for v_i=-1:-1:-vmaxif left_2(i)+v_i<1s{1}(left_1(i),left_2(i))=0;s{2}(left_1(i),left_2(i))=0;%s{3}(left_1(i),left_2(i))=0;leave=1;break;endlight=~((flag==2)&(m(left_1(i),left_2(i)+v_i)==6));if s{1}(left_1(i),left_2(i)+v_i)==0 && lightv=v_i;if m(left_1(i),left_2(i)+v_i)==5 ...||m(left_1(i),left_2(i)+v_i)==6incross=1;break;endelsebreak;endendif leave==0 %没有离开才有这些v=max(v,s{2}(left_1(i),left_2(i))-1);s{1}(left_1(i),left_2(i))=0;s{1}(left_1(i),left_2(i)+v)=1;if incross~=1s{2}(left_1(i),left_2(i)+v)=v;elses{2}(left_1(i),left_2(i)+v)=min(s{2}(left_1(i),left_2(i)),v);ends{2}(left_1(i),left_2(i))=0;endend%下行down=s{1}.*(m==3);[down_1,down_2]=find(down);[down_2,i_r]=sort(down_2,'descend');down_1=down_1(i_r);for i=1:length(down_1)v=0;leave=0;incross=0;for v_i=1:vmaxif down_1(i)+v_i>as{1}(down_1(i),down_2(i))=0;%s{2}(down_1(i),down_2(i))=0;s{3}(down_1(i),down_2(i))=0;leave=1;break;endlight=~((flag==1)&(m(down_1(i)+v_i,down_2(i))==6));if s{1}(down_1(i)+v_i,down_2(i))==0 && lightv=v_i;if m(down_1(i)+v_i,down_2(i))==5 ...||m(down_1(i)+v_i,down_2(i))==6incross=1;break;endelsebreak;endendif leave==0 %没有离开才有这些v=min(v,s{3}(down_1(i),down_2(i))+1);s{1}(down_1(i),down_2(i))=0;s{1}(down_1(i)+v,down_2(i))=1;if incross~=1s{3}(down_1(i)+v,down_2(i))=v;elses{3}(down_1(i)+v,down_2(i))=max(s{3}(down_1(i),down_2(i)),v);ends{3}(down_1(i),down_2(i))=0;endend%上行up=s{1}.*(m==4);[up_1,up_2]=find(up);[up_2,i_r]=sort(up_2);up_1=up_1(i_r);for i=1:length(up_1)v=0;leave=0;incross=0;for v_i=-1:-1:-vmaxif up_1(i)+v_i<1s{1}(up_1(i),up_2(i))=0;%s{2}(up_1(i),up_2(i))=0;s{3}(up_1(i),up_2(i))=0;leave=1;break;endlight=~((flag==1)&(m(up_1(i)+v_i,up_2(i))==6));if s{1}(up_1(i)+v_i,up_2(i))==0 && lightv=v_i;if m(up_1(i)+v_i,up_2(i))==5 ...||m(up_1(i)+v_i,up_2(i))==6incross=1;break;endelsebreak;endendif leave==0 %没有离开才有这些v=max(v,s{3}(up_1(i),up_2(i))-1);s{1}(up_1(i),up_2(i))=0;s{1}(up_1(i)+v,up_2(i))=1;if incross~=1s{3}(up_1(i)+v,up_2(i))=v;elses{3}(up_1(i)+v,up_2(i))=min(s{3}(up_1(i),up_2(i)),v);ends{3}(up_1(i),up_2(i))=0;endend%路口s=cross(s,m,p);end??
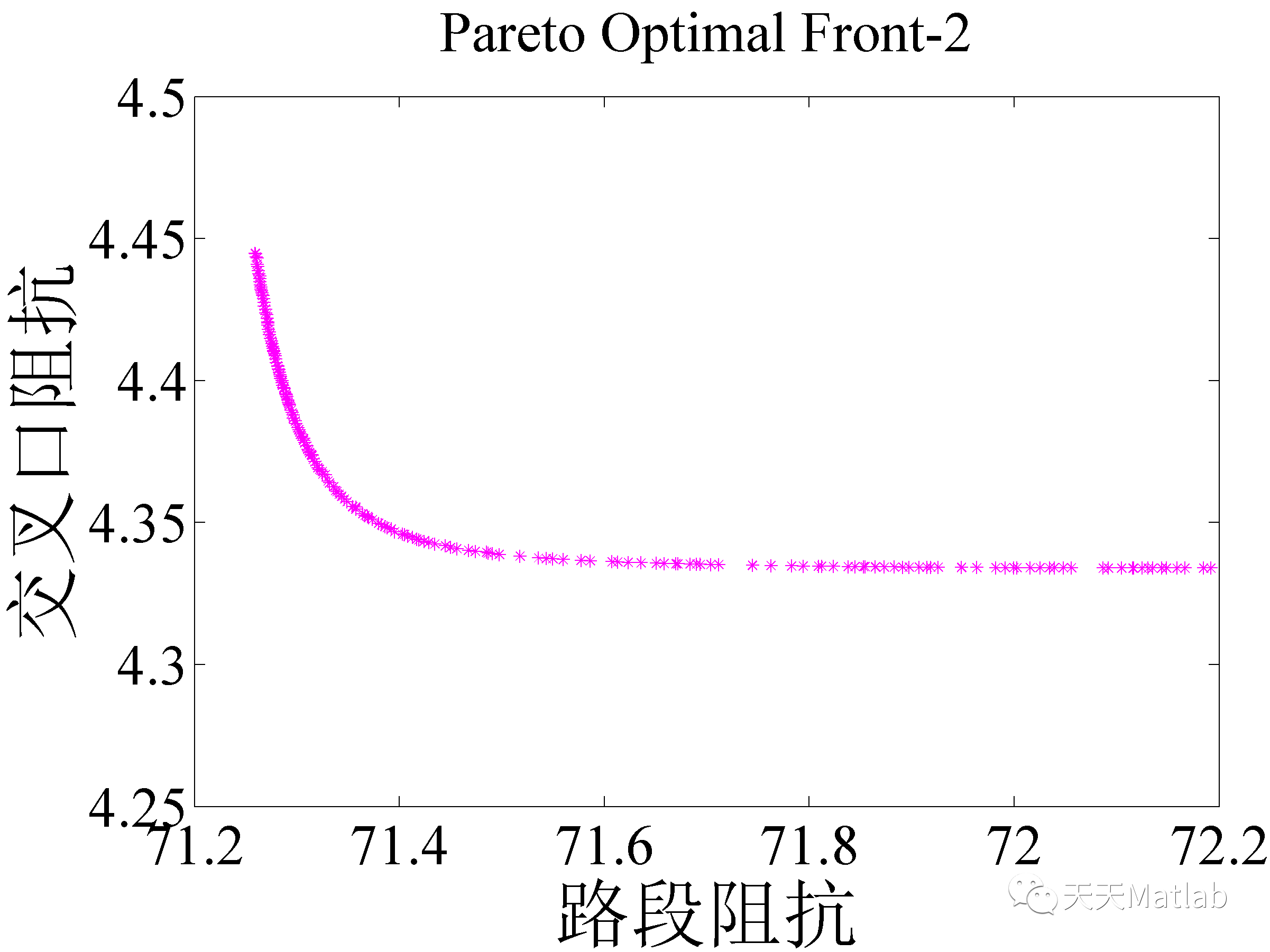
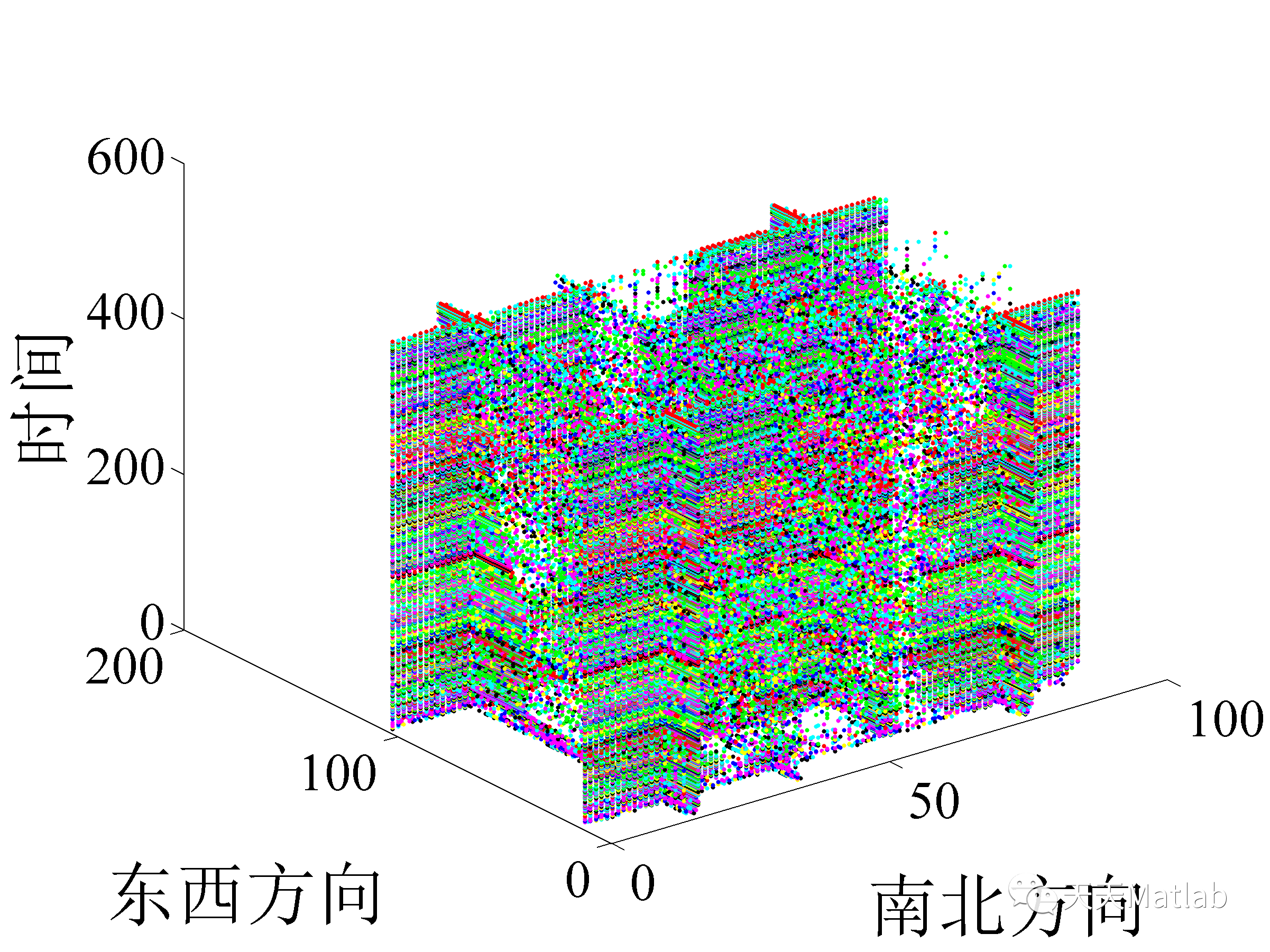
3 仿真结果

4 参考文献
[1]黄妍慧. 基于元胞自动机方法的交叉行人流动态特性模拟和解析研究[D]. 合肥工业大学.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。