贪心算法(greedy algorithm),是用计算机来模拟一个“贪心”的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。
贪心算法,又名贪婪法,是寻找最优解问题的常用方法,这种方法模式一般将求解过程分成若干个步骤,但每个步骤都应用贪心原则,选取当前状态下最好/最优的选择(局部最有利的选择),并以此希望最后堆叠出的结果也是最好/最优的解。
贪心算法的基本思路:
??? 1.建立数学模型来描述问题。
??? 2.把求解的问题分成若干个子问题。
??? 3.对每一子问题求解,得到子问题的局部最优解。
4.把子问题的解局部最优解合成原来解问题的一个解。
示例1
老魏开了间小店,不能电子支付,钱柜里的货币只有 25 分、10 分、5 分和 1 分四种硬币,如果你是售货员且要找给客户42分钱的硬币,如何安排才能找给客人的钱既正确且硬币的个数又最少?
解析:
(1)建立数学模型
选择硬币面额的和= 42.
(2)问题拆分为子问题
选择硬币进行支付的过程,可以划分为n个子问题:即每个子问题对应为:
在未超过51的前提下,在剩余的硬币中选择一张硬币。
(3)制定贪心策略,求解子问题
初次先找给顾客25分,还差顾客sum_money=42-25=17,不能再选25分的;
选10分的,此时sum_money=17-10=7,还能够选10分的;
选5分的,此时sum_money=7-5=2,不能再选5分的;
选1分的,此时sum_money=2-1=1。还能够选10分的;
sum_money=1-1=0至此,顾客收到零钱,交易结束。
(4)将所有解元素合并为原问题的解
此时42分,分成了1个25,2个10,1个5,1个2,共四枚硬币。
源码
#include<iostream>
using namespace std;
#define ONEFEN 1
#define FIVEFEN 5
#define TENFEN 10
#define TWENTYFINEFEN 25
int main()
{
int sum_money=42;
int num_25=0,num_10=0,num_5=0,num_1=0;
//不断尝试每一种硬币
while(sum_money>=TWENTYFINEFEN) { num_25++; sum_money -=TWENTYFINEFEN; }
while(sum_money>=TENFEN) { num_10++; sum_money -=TENFEN; }
while(sum_money>=FIVEFEN) { num_5++; sum_money -=FIVEFEN; }
while(sum_money>=ONEFEN) { num_1++; sum_money -=ONEFEN; }
//输出结果
cout<< "25分硬币数:"<<num_25<<endl;
cout<< "10分硬币数:"<<num_10<<endl;
cout<< "5分硬币数:"<<num_5<<endl;
cout<< "1分硬币数:"<<num_1<<endl;
return 0;
}
示例2
假定一个有n个活动(activity)的集合S={a1,a2,....,an},这些活动使用同一个资源(例如同一个阶梯教室),而这个资源在某个时刻只能供一个活动使用。每个活动ai都有一个开始时间si和一个结束时间fi,其中0<=si<fi<正无穷。如果被选中国,任务ai发生在半开时间区间[si,fi)期间。如果两个活动ai和aj满足[si,fi)和[sj,fj)不重叠,则称它们是兼容的。也就说,若si>=fj或sj>=fi,则ai和aj是兼容的。在活动选择问题中,我们希望选出一个最大兼容活动集。假定活动已按结束时间fi的单调递增顺序排序:
?? f1<=f2<=f3<=f4<=...<=fn-1<=fn
考虑下面的活动集合: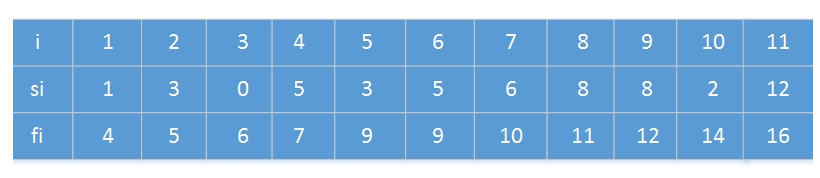
我们可以给出贪心算法在解决这个问题的两种方式:递归和迭代方式,两种算法都是按照自顶向下来求解问题的。
源代码如下:
#include <iostream>
#include <vector>
using namespace std;
void swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
int Adjust_Arr(int* a, int* b, int start, int end) {
int p = start;
int q = end;
int i = p - 1;
int j = p;
int key = a[q];
while (j < q) {
if (a[j] >= key) {
j++;
continue;
} else {
i++;
swap(a + i, a + j);
swap(b + i, b + j);
j++;
}
}
i++;
swap(a + i, a + q);
swap(b + i, b + q);
return i;
}
void Quick_Sort(int* a, int* b, int start, int end) {
if (start < end) {
int mid = Adjust_Arr(a, b, start, end);
Quick_Sort(a, b, start, mid - 1);
Quick_Sort(a, b, mid + 1, end);
}
}
void Print_Arr(int* a, int len) {
for (int i = 0; i < len; i++) {
cout << a[i] << ' ';
}
cout << endl;
}
// 递归版本
void Recursive_Activity_Selector(vector<int>* A, int* s, int* f, int k, int n) {
int m = k + 1;
while (m <= n && s[m] < f[k]) {
m++;
}
if (m <= n) {
A->push_back(m);
Recursive_Activity_Selector(A, s, f, m, n);
}
}
// 迭代版本
vector<int>* Greedy_Activity_Selector(int*s, int*f, int n) {
vector<int>* A = new vector<int>;
int k = 1;
A->push_back(k);
for (int m = 2; m <= n; m++) {
if (s[m] >= f[k]) {
A->push_back(m);
k = m;
}
}
return A;
}
int main() {
int s[12] = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12 };
int f[12] = { 0, 4, 5, 6, 7, 9, 9, 10, 11, 12, 14, 16 };
//先将f按从小到大排序,s的位置随f而动
Quick_Sort(f, s, 0, 12 - 1);
//下面两句用作调用递归版本
// vector<int>* A = new vector<int>;
// Recursive_Activity_Selector(A, s, f, 0, 12 - 1); //这里下标只能取到11
//下面一句用作调用迭代版本
vector<int>* A = Greedy_Activity_Selector(s, f, 12 - 1);
cout << "===========" << endl;
vector<int>::iterator iter;
for (iter = A->begin(); iter != A->end(); iter++) {
cout << *iter << ' ';
}
cout << endl << "===========" << endl;
delete A;
return 0;
}
运行之,结果如下:
由此可知,本例中,{a1,a4,a8,a11}是一个最大集。